案例:变式题目,大多不会解答。
一节随堂课,苏教版五年级数学,“圆的面积”教学。
教师引导学生推导出“圆的面积”公式后,设计了三道练习题让学生解答。
(1)一个圆的半径是4厘米,求圆的面积;(2)一个圆的直径是6厘米,求圆的面积;(3)把一个圆剪拼成一个近似宽2厘米的长方形,求这个长方形的面积。
学生独立解答,教师巡视。前两题,所有学生都能应用公式正确求解,第(3)题,不少学生束手无策。
……
课后,与上课老师交流,听听意见。
上课老师如是说,“我觉得第(3)题,只是变换了说法而已,比较简单。在推导圆的面积公式过程中,我该讲的都讲了,该注意的地方也强调了,学生也应该理解了。”
思考:不会解答,缘于缺少反思。
“学生真正理解了?如果理解了怎么会束手无策……?”仔细分析,第(3)题,其实是一道围绕圆的面积公式推导过程所设计的变式题。这里的“宽2厘米”就是原来圆的半径,求近似长方形的面积就是求原来圆的面积。学生解答不出来,问题不在于题目本身简单不简单,主要是学生在解答过程中不能把“ 长方形的宽2厘米” 与“圆的半径2厘米”自然联系起来,束手无策,情理之中。
不难发现,对于圆的面积公式推导过程,学生只是在不经意间经历了,在老师一问一答的过程中被动地经历了,也就是学生在教师“规范”的指令下完成了相应的数学活动。对于怎么想到把“圆”转化成“长方形“,把“圆”转化成近似的“长方形”的念头是怎样产生的,学生云里雾里。整个“圆面积公式”的推导过程,学生的理解是片面的、粗浅的理解,是不全面、不深刻的。因此,案例中直接利用公式求圆的面积的简单题目,学生轻车熟路;对于变式题,学生不能在“ 长方形的宽” 和“圆的半径”之间进行有机联系、自然转换,由于缺少反思,解答不出不足为奇。
策略:自觉反思,让学习走向深刻。
没有反思的学习是不深刻的。亚里士多德曾说:“未经审视的生活是不值得过的。”费赖登塔尔也说:“没有反思,学生的理解就不可能从一个水平升华到更高的水平。”“圆的面积”教学片段,如果教师引导学生再向前走上一步,利用反思性策略进行学习反思,教学效果就会更好。
那么,如何引导学生利用反思性策略进行学习,养成自觉反思意识,提高反思水平呢?笔者结合“圆的面积”教学谈谈自己的认识。
一、回顾性反思——让结论的来龙去脉更清晰
教学中,教师启发学生推导公式、研究法则、寻找规律、探究性质时,当得出了新的结论,不是大功告成,万事大吉,而要趁热打铁,引导学生进行回顾性反思,以便形成知识链,建构知识块,联结知识网,丰富和完善学生认知,让结论的来龙去脉更清晰。
“圆的面积”教学,推导得出圆的面积公式后,可以分四个层次进行反思:①我们是怎样想到把“圆”转化成“长方形”的;②我们是怎样把“圆”剪拼成“长方形”的;③推导圆的面积公式运用了哪些数学知识,采用了哪些数学思想;④推理的过程是否严密合理,是否还有其他方法。经过层层递进式反思,学生眼前一定能浮现出“圆”转化成近似“长方形”的过程,想到“圆”,脑中会立即呈现剪拼的“长方形”,自然打通“圆”和“长方形”两个图形之间转化的思维通道,消除束手无策的尴尬境地。
二、诊断性反思——让练习的习得过程更有效
课堂上,为了让学生巩固知识、形成技能,发展智力、提高能力,及时组织学生进行练习很有必要。现实情况是不少教师重“练”轻“评”。评讲环节,蜻蜓点水,草草收场,失去了练习的真正意义和价值。
要改变这种状况,教师可在学生练习之后,通过小组交流或自主评析的方法让学生反思整个练习的过程,明晰“成败得失”。练习成功,让学生总结经验,体验成功,享受快乐;练习失败,让学生找准病因,及时纠正,自我反省。经常进行这样深层次的诊断性反思,能改变为练习而练习的现象,养成学生良好的解题习惯和自觉反省意识,不断提高练习质量,提升教学效益。
在“圆的面积”教学案例中,学生解题束手无策,可以引导学生这样反思:第(1)题和第(2)题,我们能迅速解答,有什么秘诀吗?而第(3)题虽然简单,但我们无从下手,原因何在?平时学习中,还需要注意什么?通过正反两方面的反思,让学生明白,对于识记性的题目,直接利用公式就能迎刃而解;对于变异性的题目,需要在已有知识经验的基础上加强联系和转换,方能“峰回路转”。因此,在进行“圆的面积”教学时,可以给足时间,让学生在教师的启发和引导下,自主探究,拓展解题思路,疏通解题渠道,体验习得过程,从而使练习更有效。
三、比较性反思——让知识的勾连融通更便捷
在“圆的面积”教学中,老师设计了这样一道题目(如下图1):已知正方形的面积是5平方厘米。求圆的面积。
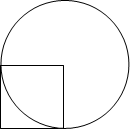
图 1
组织学生练习,有两种声音。
声音1:这道题目不好解答。因为要求圆的面积,必须先知道圆的半径。而圆的半径就是正方形的边长。正方形的面积是5平方厘米,也就是正方形的边长×正方形的边长=5平方厘米,那么多少乘多少等于5,没有办法知道。正方形的边长求不出来,圆的面积也就无法求。
声音2:正方形的面积是5平方厘米,也就是正方形的边长×正方形的边长是5平方厘米。而正方形的边长×正方形的边长也就是圆的半径×圆的半径。正方形的边长×正方形的边长是5平方厘米,圆的半径×圆的半径也就是5平方厘米。所以圆的面积可以直接这样求:3.14×5=15.7(平方厘米)。
第一种声音,学生是根据常规思维进行思考的。这样思考行不通,思维受阻。第二种声音,学生另辟蹊径,从整体上把握圆的面积计算公式,很快求得答案。
两种声音的出现带给了我们的思考。教师平时在组织学生进行基本练习的同时,还需要加强变式练习(如以上题型),勾连图形与图形之间的联系,从整体上理解公式、运用公式,培养思维的灵活性和深刻性。
以上题目,如果再进行以下变式与比较,学生的认知水平较前会有大幅度提高,真正实现知识的勾连与融通。
如下图2:已知正方形的面积是5平方厘米,求圆的面积。
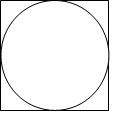
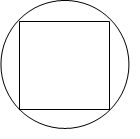
图 2 图 3
如上图3:正方形的面积是5平方厘米,求圆的面积。
通过以上三道题的解答与分析、比较与反思,学生定会不断增强运用公式解决与图形有关问题的能力,因此,教师的教学不能教条,学生的学习需要反思,只有这样,“教”与 “学”才能相得益彰。
